符號的發明及使用比數字要晚,但其數量卻超過了數字。現在常用的數學符號已超過了200個,其中,每一個符號都有一段有趣的經歷。
基本介紹
- 中文名:數學符號
- 外文名:mathematical notation
- 領域:數學
- 目的:適應數學的抽象與形式化的特點
- 實質:人類理性思維與抽象思維的產物
發展歷程,符號種類,數量符號,運算符號,關係符號,結合符號,性質符號,省略符號,排列組合符號,離散數學符號,希臘字母簡表,意義,套用,其他信息,
發展歷程
例如曾經有好幾種,目前通用“ ”號。“ ”號是由拉文“et”(“和”的意思)演變而來的。十六世紀,義大利科學家用“plu”(“加”的意思)的第一個字母表示加,草為“μ”最後都變成了“ ”號。“-”號是從拉丁文“minus”(“減”的意思)演變來的,一開始簡寫為m,再因快速書寫而簡化為“-”了。數學符號
也有人說,賣酒的商人用“-”表示酒桶里的酒賣了多少。以後,當把新酒灌入大桶的時候,就在“-”上加一豎,意思是把原線條勾銷,這樣就成了個“ ”號。
到了十五世紀,德國數學家魏德美正式確定:“ ”用作加號,“-”用作。
曾經用過十幾種,現代數學通用兩種。一個是“×”,最早是英國數學家奧屈特1631年提出的;一個是“·”,最早是英國數學家赫銳奧特首創的。德國數學家認為:“×”號像拉丁字母“x”,可能引起混淆而加以反對,並贊成用“·”號(事實上點乘在某些情況下亦易與小數點相混淆)。後來他還提出用“∩“表示。這個符號在現代已套用到中了。
到了十八世紀,美國數學家歐德萊確定,把“×”作為乘號。他認為“×”是“ ”的旋轉變形,是另一種表示增加的符號。
“÷”最初作為減號,在歐洲大陸長期流行。直到1631年英國數學家奧屈特用“:”表示或,另外有人用“-”(除線)表示除。後來數學家拉哈在他所著的《》里,才根據民眾創造,正式將“÷”作為。
平方根號曾經用拉丁文“radix”(根)的首尾兩個字母合併起來表示,十七世紀初葉,法國數學家在他的《》中,第一次用“√”表示。“√”是由拉丁字線“r”的變形,“ ̄”是括線。
十六世紀法國數學家維葉特用“=”表示兩個量的差別。可是英國牛津大學數學、修辭學教授列考爾德覺得:用兩條平行而又相等的直線來表示兩數相等是最合適不過的了,於是等於符號“=”就從1540年開始使用起來。
1591年,法國數學家在中大量使用這個符號,才逐漸為人們接受。十七世紀德國廣泛使用了“=”號,他還在幾何學中用“∽”表示,用“≌”表示。
大於號“>”和小於號“<”,是1631年英國著名家赫銳奧特創用。至於“≥”、“≤”、“≠”這三個符號的出現,是很晚很晚的事了。“{}”和“[]”是代數創始人之一魏治德創造的。
任意號(全稱量詞)∀來源於英語中的arbitrary一詞,因為小寫和大寫均容易造成混淆,故將其單詞首字母大寫後倒置。同樣,存在號(存在量詞)∃來源於exist一詞中e的反寫。
符號種類
數量符號
如:i, ,a,x,e,π。詳見下。 x軸y軸
x軸y軸
 x軸y軸
x軸y軸運算符號
如( ),(-),(×或·),(÷或/),兩個的(∪),(∩),(√ ̄),(log,lg,ln,lb),(:),符號| |,(d),積分(∫),閉合曲面(曲線)(∮)等。
關係符號
如“=”是,“≈”是近似符號(即),“≠”是,“>”是符號,“<”是符號,“≥”是大於或等於符號(也可寫作“≮”,即不小於),“≤”是小於或等於符號(也可寫作“≯”,即不大於),“→ ”表示變數變化的趨勢,“∽”是相似符號,“≌”是全等號,“∥”是平行符號,“⊥”是垂直符號,“∝”是符號(表示時可以利用關係),“∈”是屬於符號,“⊆”是包含於符號,“⊇”是包含符號,“|”表示“能”(例如a|b 表示“a能整除b”,而 ||b表示r是a恰能整除b的最大冪次),x,y等任何字母都可以代表。
結合符號
如小“()”,“[ ]”,“{ }”,橫線“—”,比如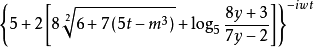 。
。
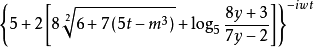
性質符號
如“ ”,“-”,“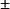 ”(以及與之對應使用的負正號“
”(以及與之對應使用的負正號“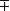 ”)
”)
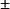
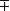
省略符號
如(△),直角三角形(△),()(見),

(),x的(),(),(∠),
因為
所以
,連加:,求積,連乘:,從n個元素中取出r個元素所有不同的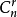 (n元素的總個數;r參與選擇的元素個數),
(n元素的總個數;r參與選擇的元素個數),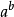 等。
等。
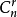
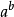
排列組合符號
c
a (或p)
n 元素的總個數
r 參與選擇的元素個數
! ,如5!=5×4×3×2×1=120,規定0!=1
!! 半階乘(又稱),例如7!!=7×5×3×1=105,10!!=10×8×6×4×2=3840
∑連加
離散數學符號
∀
∃
├ 斷定符(公式在l中可證)
╞ 滿足符(公式在e上有效,公式在e上可滿足)
﹁ 命題的“非”運算,如為﹁p
∧ 命題的“”(“”)運算
∨ 命題的“”(“”,“可兼或”)運算
→ 命題的“條件”運算
↔ 命題的“雙條件”運算的
p<=>q 命題p與q的
p=>q 命題p與q的關係(p是q的,q是p的)
a* 公式a的對偶公式,或表示a的(此時亦可寫為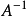 )
)
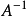
wff
iff
↑ 命題的“” 運算( “” )
↓ 命題的“”運算( “” )
□ 詞“必然”
◇ 模態詞“可能”
∅
∈ 屬於(如"a∈b",即“a屬於b”)
∉ 不屬於
p(a) 集合a的
|a| 集合a的點數
r2=r○r [r=r○r] 關係r的“複合”
ℵ aleph,阿列夫
⊆ 包含
⊂(或⫋) 真包含
另外,還有相應的⊄,⊈,⊉等
∪ 集合的並運算
u(p)表示p的領域
∩ 集合的交運算
-或\ 集合的差運算
⊕集合的對稱差運算
〡 限制
集合關於關係r的
a/r 集合a上關於r的
[a] 元素a產生的
i環,理想
z/(n) 模n的集合
r(r) 關係 r的自反
s(r) 關係 r的對稱閉包
cp 命題演繹的定理(cp 規則)
eg 存在推廣規則(引入規則)
es 存在量詞特指規則(存在量詞消去規則)
ug 全稱推廣規則(引入規則)
us 全稱特指規則(全稱量詞消去規則)
r 關係
r
r○s 關係 與關係 的複合
domf 函式 的(前域)
ranf 函式 的
f:x→y f是x到y的
(x,y) x與y的,有時為避免混淆,使用(x,y)
[x,y] x與y的,有時為避免混淆,使用(x,y)
ah(ha) h關於a的左(右)
ker(f) 同態映射f的核(或稱f同態核)
[1,n] 1到n的集合
d(a,b),|ab|,或ab 點a與點b間的距離
d(v) 點v的
g=(v,e) 點集為v,邊集為e的圖g
w(g) 圖g的數
k(g) 圖g的點
δ(g) 圖g的最大點度
a(g) 圖g的
p(g) 圖g的
m(g) 圖g的
c 集
i 集
n ,非負整數集(包含元素"0")
n*(n ) 正自然數集,正整數集(其中*表示從集合中去掉元素“0”,如r*表示非零實數)
p ()集
q 集
r 集
z 集
set 集範疇
top 拓撲空間範疇
ab 交換群範疇
grp 群範疇
mon 單元半群範疇
ring 有單位元的(結合)環範疇
rng 環範疇
crng 交換環範疇
r-mod 環r的左模範疇
mod-r 環r的右模範疇
field 域範疇
poset 偏序集範疇
希臘字母簡表
序號 | 大寫 | 小寫 | 英語音標註音 | 英文 | 漢字注音 | 常用指代意義 |
1 | α | α | /'ælfə/ | alpha | 阿爾法 | 角度,係數,角加速度,第一個 |
2 | β | β | /'bi:tə/或/'beɪtə/ | beta | 貝塔 /畢塔 | 磁通係數,角度,係數 |
3 | γ | γ | /'gæmə/ | gamma | 伽瑪 /甘瑪 | 電導係數,角度,比熱容比 |
4 | δ | δ | /'deltə/ | delta | 得爾塔 /岱歐塔 | 變化量,化學反應中的加熱,屈光度,一元二次方程中的判別式 |
5 | ε | ε | /'epsɪlɒn/ | epsilon | 埃普西龍 | 對數之基數,介電常數 |
6 | ζ | ζ | /'zi:tə/ | zeta | 澤塔 | 係數,方位角,阻抗,相對黏度 |
7 | η | η | /'i:tə/ | eta | 伊塔 /誒塔 | 遲滯係數,效率 |
8 | θ | θ | /'θi:tə/ | theta | 西塔 | 溫度,角度 |
9 | ι | ι | /aɪ'əʊtə/ | iota | 埃歐塔 | 微小,一點 |
10 | κ | κ | /'kæpə/ | kappa | 堪帕 | 介質常數,絕熱指數 |
11 | ∧ | λ | /'læmdə/ | lambda | 蘭姆達 | 波長,體積,導熱係數 |
12 | μ | μ | /mju:/ | mu | 謬/穆 | 磁導係數,微,動摩擦系(因)數,流體動力黏度,微(千分之一),放大因數(小寫) |
13 | ν | ν | /nju:/ | nu | 拗/奴 | 磁阻係數,流體運動粘度,光子頻率,化學計量數 |
14 | ξ | ξ | 希臘/ksi/ 英美/ˈzaɪ/或/ˈsaɪ/ | xi | 可西 /賽 | 隨機變數,(小)區間內的一個未知特定值 |
15 | ο | ο | /əuˈmaikrən/ 或/ˈɑmɪˌkrɑn/ | omicron | 歐(阿~)米可榮 | 高階無窮小函式 |
16 | ∏ | π | /paɪ/ | pi | 派 | 求積,圓周率(=圓周÷直徑≈3.1416),π(n)表示不大於n的質數個數 |
17 | ρ | ρ | /rəʊ/ | rho | 柔/若 | 電阻係數,柱坐標和極坐標中的極徑,密度 |
18 | ∑ | σ,ς | /'sɪɡmə/ | sigma | 西格瑪 | 求和,表面密度,跨導,正應力 |
19 | τ | τ | /tɔ:/或/taʊ/ | tau | 套/駝 | 時間常數,切應力,2π(兩倍圓周率) |
20 | υ | υ | /ˈipsɪlon/ 或/ˈʌpsɪlɒn/ | upsilon | 宇(阿~)普西龍 | 位移 |
21 | φ | φ | /faɪ/ | phi | 弗愛 /弗憶 | 磁通,輔助角,透鏡焦度,熱流量 |
22 | χ | χ | /kaɪ/ | chi | 凱/柯義 | 統計學中有卡方(χ^2)分布 |
23 | ψ | ψ | /psaɪ/ | psi | 賽/普賽/普西 | 角速,介質電通量,ψ函式 |
24 | ω | ω | /'əʊmɪɡə/ 或/oʊ'meɡə/ | omega | 歐米伽 /歐枚嘎 | 歐姆(電阻單位),角速度,交流電的電角度,化學中的質量分數 |
意義
符號(symbol) 意義(meaning)
= is equal to
≠ is not equal to
≈ approximately equal to
< is less than
> is greater than
// is parallel to
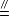
⊥
≥ 大於或等於 is greater than or equal to
≤ 小於或等於 is less than or equal to
≡ 恆等於或
π 約為3.1415926536ratio of circumference to diameter; pi
e 約為 2.7182818285natural constant
|x| 或(複數的)absolute value of x

∽ is similar to
≌ is equal to(especially for geometric figure)
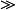
<< 遠小於
∪
∩
⊆ 於
∈
⊙
/ 除,求商值,部分程式語言中理解為
α,β,γ,φ… ;
(包括正無窮大 ∞與負無窮大-∞)
lnx 以e為底的()
lgx 以10為底的對數()
lbx 以2為底的對數
lim 求極限
floor(x) 或[x],亦可寫為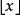 下取整函式(直譯為“地板函式”),又稱
下取整函式(直譯為“地板函式”),又稱
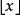
ceil(x) 亦可寫為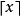 上取整函式(直譯為“天花板函式”)
上取整函式(直譯為“天花板函式”)
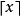
x mod y模,求
x-floor(x) 或{x} 表示x的小數部分
dy,df(x) 函式y=f(x)的微分(或線性主部)
∫f(x)dx ,函式f的全體原函式
平面二維k-ε紊流模型不同壁函式的對比及研究
函式f從a到b的
表示i從m到n逐一遞增對連加(sigma:∑ )
表示i從m到n逐一遞增對連乘求積 (pi:π)
套用
crng 交換環範疇
r-mod 環r的左模範疇
field 域範疇
poset 偏序集範疇
其他信息
在中可以插入一般套用條件下的所有數學符號,以word2010及2010版以上軟體為例介紹操作方法:第1步,打開word2010文檔視窗,單擊需要添加數學符號的公式,並將插入條游標定位到目標位置。第2步,在“公式工具/設計”功能區的“符號”分組中,單擊“其他”按鈕打開符號面板。默認顯示的“基礎數學”符號面板。用戶可以在“基礎數學”符號面板中找到最常用的數學符號。同樣地,alt 41420(即壓下alt不放,依次按41420(小鍵盤),最後放開alt 就可以打出 √。
